Abstracts

Rational Approximation:

    - Bernhard Beckermann (U Lille)
Rational approximation I+II: How well do rational functions approach more complicated functions?  
In many applications, one wishes to replace ``complicated'' functions $f$ by more simple ones, say, rational functions $r$, where it is desired that $r$ is both of small degree and attains a small error $|f-r|$ in some subset of the complex plane. In these lectures we will discuss the rate of convergence of best rational approximants. We first give numerical results and error bounds for some very explicit functions $f$. Subsequently we discuss three general classes of functions, namely Markov functions, meromorphic functions, and algebraic functions. Interestingly enough, the poles of our rational approximants often match the singularities of $f$, including branch cuts. One of the main tools will be logarithmic potential theory, that is, electrostatics in the plane.

    - Stefan Güttel (U Manchester)
Rational approximation III+IV: Computational methods and applications
In these two lectures we will focus on algorithmic aspects of rational approximation, discussing how different formulations of approximation problems can form the basis of powerful methods to compute best or near-best rational approximants. Particular emphasis will be placed on rational Krylov methods and rational approximants with pre-assigned poles. We will illustrate some of the theoretical findings from the first part of the course and highlight important effects that arise when the set of approximation is discrete, not continuous. Finally, we explain how rational functions naturally arise in applications such as model order reduction, nonlinear eigenvalue problems, and matrix function computations. 


Computational Mathematics of Life Sciences:

    - Susanna Röblitz (University of Bergen)
Talk 1: Metastability in biological systems
Multistability plays an essential role in the dynamics of living cells and organisms, and the systems can instantaneously switch between alternate states in a reversible or irreversible way. This phenomenon is known as metastability. For example, such dynamics of gene-regulatory networks is linked to cellular phenotype transitions that can diversify otherwise identical cell-populations. In this talk, I'll explain a numerical method to analyze metastability in complex biological systems, known as Markov state modelling, and exemplify its application within different mathematical modelling frameworks.

Key publications:
A.-S. Frank, K. Larripa, H. Ryu, S. Röblitz. Macrophage phenotype transitions in a stochastic gene-regulatory network model. Journal of Theoretical Biology 575:111634, 2023. https://doi.org/10.1016/j.physbeh.2022.114034

A.-S. Frank, K. Larripa, H. Ryu, R. G. Snodgrass, S. Röblitz. Bifurcation and sensitivity analysis reveal key drivers of
multistability in a model of macrophage polarization. Journal of Theoretical Biology, 2020. https://doi.org/10.1016/j.jtbi.2020.110511

S. Röblitz and M. Weber. Fuzzy spectral clustering by PCCA+: application to Markov state models and data classification. Advances in Data Analysis and Classification 7(2):147–179, 2013. doi: 10.1007/s11634-013-0134-6.
Talk 2: Mathematical modelling of hormonal regulation

Hormones are signaling molecules that exert their effects far from their site of production, thus enabling communication between organs and tissues. Hormones regulate a wide range of processes including, for example, metabolism, stress induction, and reproduction. Much hormonal activity is characterized by oscillatory behavior, with the period of oscillation ranging from milliseconds to days. This has significant implications for the treatment of hormonal abnormalities with drug therapies. The complexity of the endocrine system and the limited quantity and quality of data are major obstacles for constructing quantitative models of hormonal control. In this talk, I will review our
work on the development of a mathematical model for the female menstrual cycle, highlighting the fit-for-purpose principle and the potential for translational research.
Key publications:
S. Fischer-Holzhausen, S. Röblitz. Hormonal regulation of ovarian follicle growth in humans: Model-based exploration of cycle variability
and parameter sensitivities. Journal of Theoretical Biology 547:111150, 2022. https://doi.org/10.1016/j.jtbi.2022.111150

S. Fischer, R. Ehrig, S. Schäfer, E. Tronci, T. Mancini, M. Egli, F. Ille, T. H. C. Krüger, B. Leeners, S. Röblitz. Mathematical Modeling and
Simulation Provides Evidence for New Strategies of Ovarian Stimulation. Frontiers in Endocrinology 12:613048, 2021. https://doi.org/10.3389/fendo.2021.613048

A. Lange, R. Schwieger, J. Plöntzke, S. Schäfer and S. Röblitz. Follicular competition in cows: The selection of dominant follicles as a
synergistic effect. Journal of Mathematical Biology 78(3):579–606, 2019. doi: 10.1007/s00285-018-1284-0

S. Röblitz, C. Stötzel, P. Deuflhard, H. M. Jones, D.-O. Azulay, P. van der Graaf, and S. W. Martin. A mathematical model of the human menstrual cycle for the administration of GnRH analogues. J. Theoret. Biol. 321:8–27, 2013. https://doi.org/10.1016/j.jtbi.2012.11.020
  
 - Marie Rognes (Simula Research Laboratory, Norway)

Talk 1: "Brains in motion: computational modelling of the brain's waterscape"
Your brain has its own waterscape: whether you are reading, thinking or sleeping, fluid flows through or around the brain tissue, clearing waste in the process. These physiological processes are crucial for the well-being and function of the brain, but the precise underlying mechanisms and their association with neurodegenerative diseases such as Alzheimer's and Parkinson's disease and neurological events such as seizures remain only partially understood. Mathematical and computational modelling could play a crucial role in gaining new insight. In this talk, I will give an introduction to mathematical modelling and numerical simulation of pulsatility, fluid flow and solute transport in the human brain.

Talk 2: "Cell membranes and perivascular pathways - a finite element tale of dimensional gaps."

Structurally, brain tissue is characterized by thin cell membranes and slender vessels, defining submanifolds of codimension one and two respectively.  Functionally, your brain fundamentally relies on the transport of ions and nutrients and movement of water in and between these spaces. In this talk, I will discuss key mathematical, numerical and computational challenges associated with modelling brain mechanics and transport across scales with an emphasis on coupled systems of partial differential equations with dimensional gaps.  
 


Computational Optics:

    - Martijn Anthonissen (TU Eindhoven)
Lecture 1: Freeform design

When it gets dark and we switch on the lights, we want to be surrounded by comfortable light. The light source is typically an LED that is combined with reflectors and lenses to send the light where you want it to be. Given the light distribution of the source and the desired target distribution, what is the optical system (reflector, lens or a combination) that does the job? That is the question we need to answer!

Figure 1: The mirror is designed such that the frog-shaped source light distribution is reflected to form a prince on the target screen.

This field is freeform design and it is used for, e.g., car lights, luminaires and street lights. The optical surfaces are referred to as freeform since they do not have any symmetries. To find the optical components there are basically two approaches: direct methods and inverse methods.

In direct methods an optical component is designed in a CAD tool and the target light distribution is calculated using ray tracing. We follow many rays from the source to the target using the laws of optics (Snell’s law, law of reflection) and determine the light distribution at the target. If the obtained light distribution differs from the desired one, the CAD geometry is adjusted and a new light distribution is calculated. Because of the iterations, this is typically a slow process.

Alternatively, the problem is solved as an inverse problem. A partial differential equation can be derived that describes the shape of the lens or reflector. Our mathematical model is based on the principles of geometrical optics, formulated in terms of the optical map connecting source and target domain, and energy conservation. This leads to a fully nonlinear partial differential equation of Monge-Ampère type.

The numerical solution method is a two-stage procedure. In the first stage it computes the optical map. In the second stage it constructs the shape of the optical surface from the optical map. Both stages are solved using a least-squares method. The computation is an iterative process with fast convergence. The resulting algorithm gives accurate results and is very efficient. This is illustrated by numerical experiments.

Key publications:

  • Anthonissen, M.J.H., Romijn, L.B., ten Thije Boonkkamp, J.H.M., & IJzerman, W.L. (2021). Unified mathematical framework for a class of fundamental freeform optical systems.Optics Express, 29(20), 31650-31664. https://doi.org/10.1364/OE.438920
  • Romijn, L.B., Anthonissen, M.J.H., ten Thije Boonkkamp, J.H.M., & IJzerman, W.L. (2021). An iterative least-squares method for generated Jacobian equations in freeform optical design.SIAM Journal on Scientific Computing, 43(2), B298-B322. https://doi.org/10.1137/20M1338940
  • van Roosmalen, A.H., Anthonissen, M.J.H., IJzerman, W.L., & ten Thije Boonkkamp, J.H.M. (2023). Fresnel reflections in inverse double freeform lens design.Journal of the Optical Society of America A: Optics and Image Science, and Vision, 40(7), 1310-1318. https://doi.org/10.1364/JOSAA.490053

 

Lecture 2: Hamiltonian optics, Lie algebra and Liouville's equation

For a given optical system, the propagation of light can be described in phase space: each ray is given by its position coordinates and optical momentum. In this formulation, the evolution of the ray coordinates is governed by a Hamiltonian system.

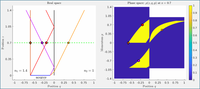
Figure 2: An optical system in real space (left) and phase space (right). Light rays in real space are points in phase space.

In imaging applications, the goal is to form a very precise image of an object and we want to minimize deviations from a linear mapping from object to image plane. Using Lie algebraic tools we find analytical expressions for these so-called aberrations.

In nonimaging applications, light propagation from source to target can be modeled as the evolution of an energy density defined on phase space. This evolution is given by Liouville’s equation of geometrical optics. We have developed advanced numerical schemes to solve it. These schemes are Discontinuous Galerkin (DG) methods combined with Arbitrary Derivative (ADER) and semi-Lagrangian techniques.

Key publications:

  • Barion, A., Anthonissen, M.J.H., ten Thije Boonkkamp, J.H.M., & IJzerman, W.L. (2023). Computing aberration coefficients for plane-symmetric reflective systems: A Lie algebraic approach.Journal of the Optical Society of America A, Optics, Image Science and Vision, 40(6), 1215-1224. https://doi.org/10.1364/JOSAA.487343
  • Barion, A., Anthonissen, M.J.H., ten Thije Boonkkamp, J.H.M., & IJzerman, W.L. (2022). Alternative computation of the Seidel aberration coefficients using the Lie algebraic method. Journal of the Optical Society of America A, Optics, Image Science and Vision, 39(9), 1603-1615. https://doi.org/10.1364/JOSAA.465900
  • van Gestel, R.A.M., Anthonissen, M.J.H., ten Thije Boonkkamp, J.H.M., & IJzerman, W.L. (2024). A hybrid semi-Lagrangian DG and ADER-DG solver on a moving mesh for Liouville's equation of geometrical optics. Journal of Computational Physics, 498, Article 112655. https://doi.org/10.1016/j.jcp.2023.112655
  • van Gestel, R.A.M., Anthonissen, M.J.H., ten Thije Boonkkamp, J.H.M., & IJzerman, W.L. (2021). An energy conservative hp-method for Liouville’s equation of geometrical optics. Journal of Scientific Computing, 89, [27]. https://doi.org/10.1007/s10915-021-01612-x